∞∞∞∞∞∞∞
[page 533, unnumbered:]
Poe’s “Eureka” Reconsidered.*
————
FOR THE NEW ECLECTIC MAGAZINE.
————
NOTWITHSTANDING Poe’s Eureka was at the time a remarkable production, it is founded upon the generally received idea of the universe being created out of nothing by a power through whose action it will finally return to nothing.
At once, my conceptions differ widely from his. I cannot conceive how anything in the universe can be created out of nihility, or without something to create from. It altogether lacks proof to sustain it; it cannot be based on anything tangible. Then again, after a universe is once created even out of nothing, I cannot conceive how it can be annihilated; neither can I conceive how the power so creating can be self-annihilated, especially if all the energies of that power were called forth in the act of creation. To undo what has been done by material force, a still greater energy is requisite to overcome the first: it being a secondary act to undo a primary, either by reversal of the primary, or new forces still more powerful acting in a contrary direction. How can this be conceived possible from our present light and knowledge? He conceives the idea of the existence of two, and only two, forces in nature, diametrically opposed to each other, as repulsion and cohesion or gravity. This may or may not be true; if true, it only confirms the views advanced many years ago by Metcalf in his work on Caloric. In it he reduces all the forces in nature to one, that of caloric, though acting under different circumstances in different directions as opposing forces or antagonistics; with strong arguments to sustain him where he says a certain amount of caloric in a solid body holds it as such by its small amount, which is cohesion; and when certain additional amounts of caloric are introduced, cohesion is sufficiently overcome to form a liquid; still further amounts, gas or vapor, when cohesion is entirely overcome, and by the identical same imponderable element or force. Whether or not there are just two distinct forces acting always in opposite directions, checkmating each other, equally potent and powerful, I shall not attempt to decide; or whether there are a number [page 534:] of forces, as we see manifested under different circumstances familiar to all men of science.
In a magnet we recognise two poles, one weaker than the other, so believed, though of the same nature. Now cut the magnet into two parts. Each part has two poles, though not of the same power as before cutting. Divide again, and the same results follow, and continue so long as subdivisions are made.
All molecules of matter either simple or compound have been conceived to be so many minute magnets, each having two poles; and when two or more molecules are united, two poles still. All masses of matter, even this great Earth, have but the two recognised poles; hence the Earth may be considered a great magnet.
One pole of the magnet, called the positive, is supposed to attract and contract; the other, called the negative, to repel and disperse.
Now reduce the magnet to a circle, and we may suppose a double current passing around this circle in opposite directions, whether with fixed poles or not I cannot say. The earth no doubt has her poles determined by solar influence. Whether or not this polar force be two distinct entities, or only one, and that one self-divisive by mutual repulsion at the centre of each mass or molecule from self dislike, has not been determined. We recognise here a repellent and an attractive, or antagonistic relations.
Can we conclude that gravity and cohesion are the same as positive polarity, and repulsion the same as negative? If so, we may conclude that all bodies occupy the same relations to each other that two magnets do, and that the positive pole of the one attracts the negative pole of the other, and vice versa; the power of such attraction and repulsion being governed by mass and distance.
Can these polarities be recognised as the dualistics of Poe? He speaks of forces being set free from one group of atoms to affect other groups, the sum of all the forces remaining the same. I cannot conceive how any group of atoms can be made to part with all their forces, or even any at all, however acted on any further than by mutual disturbance and equilibrium. I regard the forces as constant, persistent, and inherent in all bodies. I cannot conceive, like Poe, separate universes totally independent of each other; as I believe all mutually act and reäct on each other throughout space according to mass and distance: there being definite limits to these effects, time being a sequence.
I cannot conceive molecular expansion as being equal to attraction and cohesion. If so, the cosmos must have remained in chaos or vapor. Instead, we find a system of globes, still undergoing condensation by radiation of heat force, without apparently receiving in turn any equivalent expansive force.
If Poe’s views be correct, the nebular hypothesis must be a failure. Hirn’s idea of spirit being something independent of and different from force and matter, I am not ready to accede to.
Poe’s conceptions of irradiation of atoms from a common centre of the universe, which he conceives is limited, presupposes on his part the idea that all matter sprang from, nihility, or from one original atom by multiplication of that atom by Divine Will; which he beautifully [page 535:] illustrates in his description of a glass globe and irradiation commencing at the centre, sending one set of atoms just sufficient to fill the outer layer on the inside of this sphere, the force diminishing inversely as the square of the distance, and the irradiating force moving outwardly. The next layer not being the same as the first (minus mass of matter of first layer and diminished distance), the force gradually diminishes with each concentric layer interiorly until the whole globe is filled from the central starting-point uniform in density throughout, when the centrifugal and centripetal forces just counterbalance each other, and a perfect state of rest is secured. This theory is beautifully described, and seems to be the crowning point of his conceptions in relation to the creation of the universe out of nothing, only the Will of the Creator. As before stated, here I differ with him in the conception that something springs from nothing, or can so spring. His explanation of atomic attraction, gravitation, and dispersion, or balancing and checkmating of the inward and outward forces, needs no comment, as he seems to fully comprehend the whole subject as commonly understood. He seems to be fully conversant with all the knowledge extant at the time of his writing, and even in advance of his time, as stated in the review in The New Eclectic.
I differ from him in many points in cosmogony. In the first place, admitting his conceptions to be true, we have to suppose universal empty space before the cosmical beginning, and that empty space must be filled with matter created from nothing, this being the first act after the Divine Mind had predetermined so to do, the act being a secondary cause. This secondary cause would leave the universe where Laplace commences with his nebular hypothesis to create the solar system.
We may suppose the boundaries of this system to be inclosed within Poe’s hollow sphere, just filled equally from centre to circumference. Now apply Laplace’s nebular theory, until all the atoms are contracted into the present solar system, and the whole schema of the system, starting with Poe’s conception, is complete. In the first place, Poe conceives the idea that the primary or irradiating force extends to a certain limit, where it ceases, and no recoil or reaction takes place, as all the atoms would be balanced by the balancing of forces, and in order to give gravity overbalancing power the first expansive force must be withdrawn; then the law of universal gravitation begins, being most powerful in the centre, diminishing outwardly in proportion to the square of the distance. Here I shall drive a pin, and differ in toto with him and all other orthodox ideas on the subject, and shall attempt to prove my position by Poe’s own conceptions. He says that every atom or molecule attracts every other molecule in proportion to relative distance already given, in which he is undoubtedly correct. Now for the application of his theory. Supposing an atom at the surface to be acted on more powerfully directly through the centre of such spherical mass of atoms than in any other direction, which is actually true, what would we conclude? Simply that that molecule would be more powerfully drawn upon than at any other point in the interior, from the fact that all the molecules are on one side, and the greatest number on the central line through the mass all act on the one, the nearer ones more [page 536:] energetically and the remoter ones less energetically, governed by the square of the distance already explained. Now move this atom down half-way to the centre in an imaginary hole, and the mass of atoms left in the rear pulls back, and the force in front is lessened just in proportion to the amount of matter passed by or taken from the front and placed in the rear. Now move the molecule to the centre of the mass, and how then stand the forces? Is there any force at any one point more attractive than at any other? I imagine not, as here tension must be equal, and the atom would even lose its entire gravity and seem to possess no weight or specific gravity at all. Gravity here would be nil, and the tendency of a solid atom or group of solid atoms would be to the gaseous or vapory form, from the tension outwardly on all sides; unlike an atom at the surface, where the tension is all on one of its hemispheres; none in the outward direction; hence, plus at surface, and minus at centre of gravity. Two atoms of matter on opposite sides of a sphere would each be attracted by the other, though in a less degree than by any other atom on a line intervening, as all the other atoms would be nearer to each than they would be to each other governed by distance, their neutralising distance being the halfway point.
These two opposite atoms on opposite sides, by mutually attracting each other (which is wholly independent of all intervening atoms, the same as though nothing intervened) necessarily exert a certain force on all intervening atoms, forcing them together just in proportion to such force, provided there be no counteracting effect. As this attractive force from one atom to the other passes other atoms on its way, these atoms in turn exert a force back towards themselves, as no atom carries its own attractions beyond itself, but culminates in its own centre or its centre of gravity. From what has already been explained, à priori the greatest density must be sought for at the surface, and the least at the centre of gravity. Any two intermediate atoms on the central line within the surface, would be more mutually attractive than the two at the surface, as the distance would be less; though on the other hand their attraction would be weakened for each other by the sum of attraction of all molecules outside of them, which at certain points would be negatived altogether and amount to nothing.
All these facts are easily comprehended by keeping Newton’s law in view.
Let us now draw an imaginary sphere, represented by a circle thus, which we will call Poe’s
sphere, filled with solid atoms throughout, at their maximum density, though equally dense 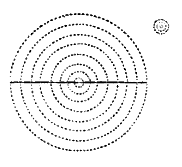 throughout.* We will draw imaginary lines across the circle, and commence our observations at
the centre with say 24 or any number of molecules. If there were no molecules outside of them, they would be mutually
attracted; supposing them touching each other, their mutual attractions would be governed by quantity [page 537:] of matter. Now surround this group of molecules to any
imaginary extent, say to the size of our earth: what then would be the mutual attractive energies of this central
group of molecules? Would their mutual attractions be the same to each other as though there were no other molecules
surrounding them? Let us investigate. When there were none surrounding them, their attractions were all retained
within themselves, now given up to surrounding molecules. Now imagine them surrounded as before stated: can all their
mutual attractive force be still retained as before? As a matter of course not; the reason is obvious. The next layer
or stratum outside would attract them, and in turn be attracted; supposing the number to be equal to the first group,
and in contact, their attractions would be mutual. So one-half of the attraction that existed in the first group would
be given up to the outside added group, the sum of the two attractions being just double what it was in the first
instance; which would lead us to conclude that the force that attracted the first group was just the same as if there
had been added an additional force equal to the first. How are the forces now exerted,
throughout.* We will draw imaginary lines across the circle, and commence our observations at
the centre with say 24 or any number of molecules. If there were no molecules outside of them, they would be mutually
attracted; supposing them touching each other, their mutual attractions would be governed by quantity [page 537:] of matter. Now surround this group of molecules to any
imaginary extent, say to the size of our earth: what then would be the mutual attractive energies of this central
group of molecules? Would their mutual attractions be the same to each other as though there were no other molecules
surrounding them? Let us investigate. When there were none surrounding them, their attractions were all retained
within themselves, now given up to surrounding molecules. Now imagine them surrounded as before stated: can all their
mutual attractive force be still retained as before? As a matter of course not; the reason is obvious. The next layer
or stratum outside would attract them, and in turn be attracted; supposing the number to be equal to the first group,
and in contact, their attractions would be mutual. So one-half of the attraction that existed in the first group would
be given up to the outside added group, the sum of the two attractions being just double what it was in the first
instance; which would lead us to conclude that the force that attracted the first group was just the same as if there
had been added an additional force equal to the first. How are the forces now exerted, 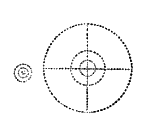 and where would be the greatest density? Undoubtedly at the surface, as no additional force had been sent through the
first group — thus — without being in turn counteracted, and even more than counteracted, leaving the
central group less dense than at first. Each atom attracts the atom nearest to itself more than it does an atom on the
outside of it, which I attempt to
and where would be the greatest density? Undoubtedly at the surface, as no additional force had been sent through the
first group — thus — without being in turn counteracted, and even more than counteracted, leaving the
central group less dense than at first. Each atom attracts the atom nearest to itself more than it does an atom on the
outside of it, which I attempt to 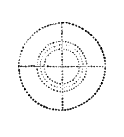 represent by the 2d diagram, which we now see representing three circles of
molecules instead of two, as in the 1st diagram. The outer circle of atoms is just equal to the two interior, and as a
matter of fact just the same mean amount of attractive force added that existed in the mass; hence the mean force is
doubled. Now supposing all the atoms touching each other as in a cannon ball, where will the greatest attractive force
exist? See last diagram; counting the molecules represented through the central line, we have 6. Now commence at one
side, and take the first molecule, whose attractive force we will call 6; the second, 5; third, 4; fourth, 3; fifth,
2; sixth and last, 1. Now commence on the opposite side, and reverse the order of numbering. We will suppose the force
of attraction to be diminished in proportion to distance from the surface inwardly towards the central attractive
point, diminishing in proportion to diminution of mass passing from the surface of the sphere to an imaginary point at
the centre. As the amount of matter on the surface exceeds the amount of matter at the centre, so are located the
forces governing the mass.
represent by the 2d diagram, which we now see representing three circles of
molecules instead of two, as in the 1st diagram. The outer circle of atoms is just equal to the two interior, and as a
matter of fact just the same mean amount of attractive force added that existed in the mass; hence the mean force is
doubled. Now supposing all the atoms touching each other as in a cannon ball, where will the greatest attractive force
exist? See last diagram; counting the molecules represented through the central line, we have 6. Now commence at one
side, and take the first molecule, whose attractive force we will call 6; the second, 5; third, 4; fourth, 3; fifth,
2; sixth and last, 1. Now commence on the opposite side, and reverse the order of numbering. We will suppose the force
of attraction to be diminished in proportion to distance from the surface inwardly towards the central attractive
point, diminishing in proportion to diminution of mass passing from the surface of the sphere to an imaginary point at
the centre. As the amount of matter on the surface exceeds the amount of matter at the centre, so are located the
forces governing the mass.
Let us now add another concentric layer on the surface of our imaginary sphere, equal in mass to all the remainder in contact. This additional amount of matter possesses the same amount of attractive force as the central mass and the mean amount of attractive force of the two will be double what it was, though differently located. As before the greatest amount of force remained at the surface, so in the last instance the greatest force comes to the surface, as the last added layer contained [page 538:] the same as the other mass; the sum of the two forces being centred on the surface gradually diminishing to the centre, where zero is reached. The power of attraction on the surface, and at any imaginary point in the interior, will be governed by the explanations already given. Hence the greatest density must be looked for on the surface, and the least at the common centre of gravity of all masses of matter. Calculate it as you will, the results will be the same: the greatest attractive force will be found where the greatest amount of matter is found, which must always be at the surface of all spheres. The relative force as already explained being in proportion to mass of matter at the surface, the greatest ending at an imaginary centre representing a single atom of matter or point. In passing from the surface towards the centre of a spherical body, attraction is lessened exactly in proportion to the amount of matter passed by or taken from the front and left in the rear. This is self-evident to any one at all conversant with Newton’s laws. In moving outwardly from the surface of any mass of matter it is entirely different, as in this instance the whole mass is left behind; hence the ratio of diminution in both cases is not the same, as in the one instance the mass is penetrated, in the other the entire mass is left behind, and all on the same side, as before stated.
We might go on adding to our spherical mass layer after layer in imagination, until we had a globe as large as our sun. Precisely the same law will follow, no matter where we stop. Even the universality of stars in their relation to each other in space may be regarded as coming under the same rule; hence there cannot be, as Poe imagines, a universal tendency to centralism or concretion by drawing together of the universe by universal gravitation. We may, however, construct in our minds a great circle on the outside of globes in contact, and all the others not included in this hollow sphere of globes forming the outer layer as being situated within, and then governed by the same law as already explained, and not as Poe supposes one conglomerate mass like our earth, or heterogeneity. Again, all spherical masses are drawn upon from the centre to the surface on all sides equally, and the interior in turn drawn upon from all sides of the surface. The latter being greatest, necessarily exerts force in proportion to quantity, zero being at the exact centre; especially in all large masses, such as independent bodies in space. The same law that governs the molecules of the smallest known globe in space, equally applies to all bodies in the universe, wherever situated. As to small atoms situated on opposite sides of a circle or sphere of large dimensions, they may be so remote from each other as not to exert any mutual attraction. Still their influence is not lost. As the atoms nearest them on each side are acted on, those in turn act on others still further in, and so atom after atom is successively acted on until the centre is reached on opposite sides. This same rule equally applies to all the masses in the universal cosmos; the stars and their attendants representing atoms in the above comparison.
S. P. CUTLER, M. D.
(To be continued.)
[[Footnotes]]
[The following footnote appears at the bottom of page 533:]
* See The New Eclectic Magazine, August, 1869.
[The following footnote appears at the bottom of page 536:]
* [Our contributor seems to overlook the fact that Poe’s hypothesis especially provides for unequal and not equal diffusion of the atoms. — ED.]
∞∞∞∞∞∞∞
Notes:
S. P. Cutler may have been Samuel Prentis Cutler (1815-1880), a dentist in Memphis, Tennessee, and chairman of the Tennessee Dental Association in the 1870s. (For a biography and portrait of Dr. Cutler, see History of Dental Surgery, 1910, 3:260-263.) He was appointed to the board of visitors of the Baltimore College of Dental Surgery in 1881. He wrote many articles about dentistry, and always signed them as “S. P. Cutler.” Although his emphasis was dentisty, he was a man of diverse interests. In spite of the promise “to be continued,” no further articles on Eureka appeared in the current magazine nor its descendant. The New Eclectic Magazine became the Southern Magazine in 1872.
∞∞∞∞∞∞∞
[S:1 - NEM, 1869] - Edgar Allan Poe Society of Baltimore - A Poe Bookshelf - Poe's Eureka Reconsidered (S. P. Cutler, 1869)